IN DRAFT MODE

Summary

Machine learning has become increasingly prominent and is widely used in various applications in practice. Despite its great success, the integrity of machine learning predictions and accuracy is a rising concern. The reproducibility of machine learning models that are claimed to achieve high accuracy remains challenging, and the correctness and consistency of machine learning predictions in real products lack any security guarantees. In this paper, the authors initiate the study of zero knowledge machine learning (ZKML) and propose protocols for zero knowledge decision tree predictions and accuracy tests.

• This paper presents a novel way of proving that a decision tree can make a correct prediction on a given data point without revealing anything about the decision tree itself. This is called a zero knowledge decision tree prediction protocol.
• The protocol has two phases: a setup phase and a proving phase. In the setup phase, the decision tree is encoded in a way that takes linear time in the size of the tree. In the proving phase, the prediction is computed in a way that only depends on the length of the prediction path and the number of features of the data point.
• The protocol uses several advanced techniques from the field of zero knowledge proofs for computations in the RAM model, but adapts them in non-black-box ways to suit the decision tree setting.
• The protocol converts the decision tree prediction to a small circuit of size $O(d + h)$, where $d$ is the number of features and $h$ is the height of the tree.
• The paper also extends the protocol to prove the accuracy of a decision tree on a testing dataset, which is called a zero knowledge decision tree accuracy protocol.
• The accuracy protocol has two optimizations that reduce the number of hashes in the zero knowledge proof backend to be exactly equal to the number of nodes in the decision tree. This number does not depend on the size of the testing dataset and can be much smaller than $2^h$ if the tree is unbalanced.
• The paper implements and evaluates both protocols on several real-world datasets. The results show that for a large decision tree with 23 levels and 1,029 nodes, it takes only 250 seconds to generate a proof for its accuracy on a testing dataset with 5,000 data points and 54 features. The proof size is 287KB, and it takes 15.6 seconds to verify it.

Citation of the Paper

Jiaheng Zhang, Zhiyong Fang, Yupeng Zhang, and Dawn Song. 2020. Zero Knowledge Proofs for Decision Tree Predictions and Accuracy. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security (CCS ‘20). Association for Computing Machinery, New York, NY, USA, 2039–2053. https://doi.org/10.1145/3372297.3417278

Zero Knowledge Proofs

The paper proposes the use of zero knowledge proofs (ZKP) to ensure the integrity of machine learning predictions and accuracy without leaking any information about the model itself. A zero knowledge proof allows a prover to produce a short proof that can convince any verifier that the result of a public function on the public input and secret input of the prover is correct. The secret input is usually referred to as the witness or auxiliary input. Zero knowledge proofs guarantee that the verifier rejects with overwhelming probability if the prover cheats on computing the result, while the proof reveals no extra information about the secret beyond the result.

• A zero-knowledge argument of knowledge for an $NP$ relation $R$ using a tuple of algorithms $(G, P, V)$ with the following properties.
• The first property of this argument system is completeness, which means that for every public parameter $pp$ generated by $G(1^λ)$, if $(x; w) ∈ R$ and $π ← P(x, w, pp)$, then the probability that Verifier $V$ accepts the proof $(x, π, pp)$ as valid is $1$.
• The second property is knowledge soundness, which ensures that any computationally-bounded prover $P^∗$ cannot convince $V$ of a false statement $(x; w) ∉ R$ without possessing a witness $w$. This property is guaranteed by the existence of a $PPT$ (probabilistic polynomial time) extractor $E$ that can extract $w$ from the executing process and randomness of $P^∗$ with negligible probability.
• The third property is zero knowledge, which means that there exists a $PPT$ simulator $S$ that can simulate the view of any verifier $V^∗$ without knowing the witness $w$ or any information about $(x; w)$. This property ensures that the proof does not reveal any information about the witness or the statement beyond what is already known.

• Finally, the definition introduces the concept of a succinct argument system, which limits the total communication between $P$ and $V$ (proof size) to be polynomial in the security parameter $λ$, the size of the input $x$, and the logarithm of the witness size $

  w

  $. This property ensures that the proof can be efficiently verified and transmitted without revealing any additional information.

Zero Knowledge Decision Tree

The model introduces a knowledgeable prover equipped with a pre-trained decision tree. The prover takes the initiative by committing to the decision tree upfront. Subsequently, the verifier raises queries about the predictions of data samples. To validate its accuracy, the prover generates a convincing proof alongside the results.

But first, let’s introduce some concepts and definitions: $F$, a finite field; $T$, a binary decision tree with a height $h$ and $N$ nodes $(N ≤ 2^h −1)$; and $D$, the test dataset containing data points with $d$ features, where each data point, $a ∈ F^d$. Moreover, we have $[M]$, representing the set of all target classifications. The decision tree algorithm, denoted as $T : F^d → [M]$, is responsible for mapping data points to their corresponding classifications. When a data point $a ∈ D$ is fed into the decision tree, $T(a) ∈ [M]$ is the classification prediction.

Embracing transparency, the scheme assumes that both parties are aware of the height (or an upper bound) of the decision tree. Furthermore, they denote $comT$ as the commitment of the decision tree, $y_a$ as the class returned by the decision tree for data point $a$, and $π$ as the proof ingeniously crafted by the prover. Finally, ${0, 1}$ represents the verifier’s output, indicating whether to accept or reject the classification and proof.

The zero-knowledge decision tree scheme (zkDT) consists of the four algorithms, $G$, $Commit$, $P$, and $V$:

1. The $pp ← zkDT.G(1^λ)$ algorithm: With the security parameter given, generate the public parameter $pp$.

2. The $comT ← zkDT.Commit(T , pp, r)$ algorithm: This step involves the prover committing to the decision tree $T$ using a random point $r$.

3. The $(y_a, π ) ← zkDT.P(T , a, pp)$ algorithm: When given a data point $a$, the decision tree algorithm is executed, producing $y_a = T(a)$ and an accompanying proof $π$.

4. The ${0, 1} ← zkDT.V(comT , h, a, y_a, π , pp)$ algorithm: At this stage, the Verifier validates the prediction of $a$, the classification $y_a$, and the proof $π$ provided by the prover.

Intuition of the construction of zkDT

Here is a sequence diagram describing the specific construction of zkDT.

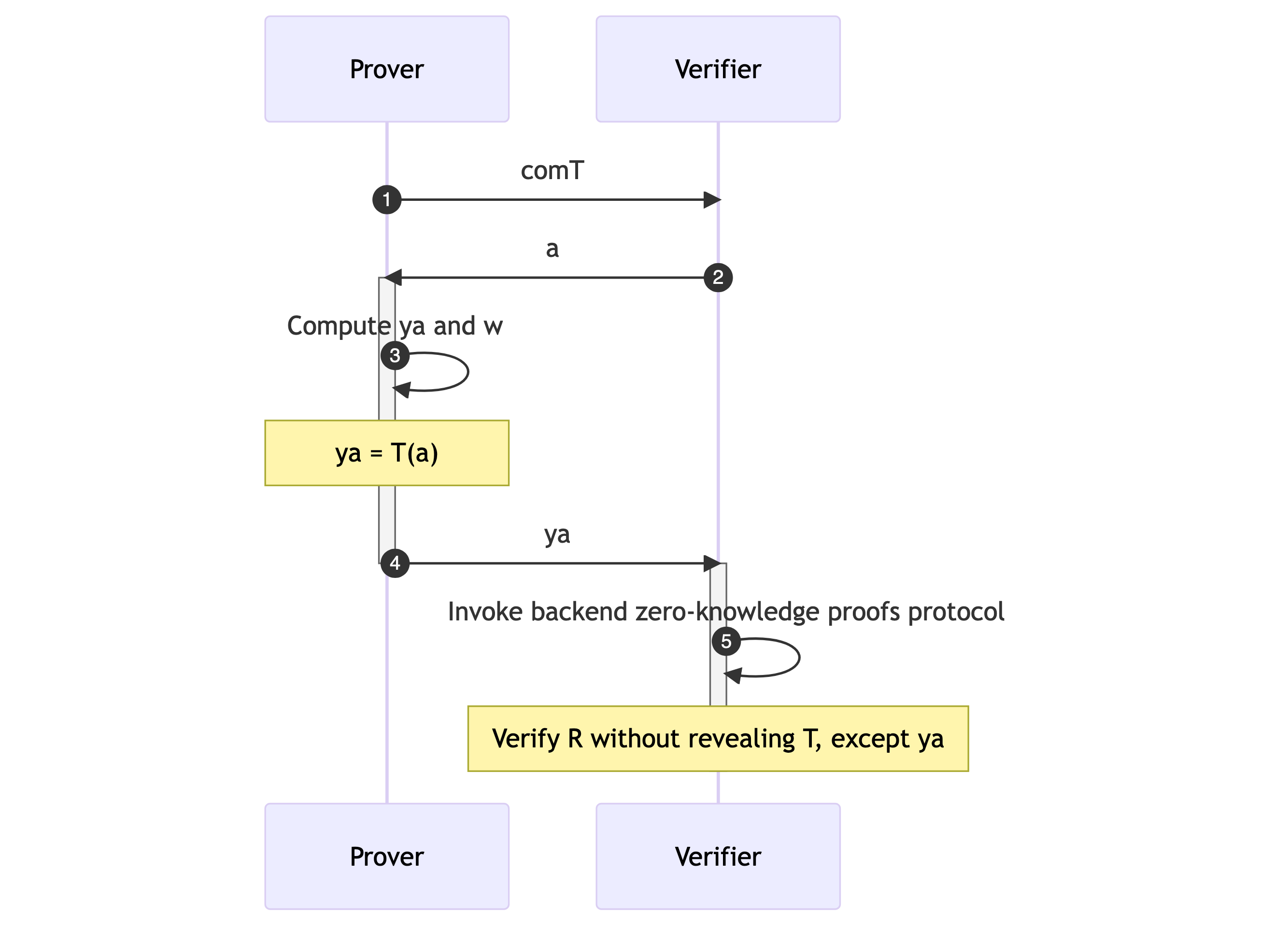
• The general idea of the construction of zkDT involves the prover $P$ sending the commitment of a decision tree $T$, $comT$, to the verifier $V$.
• After receiving the data sample $a$ from the verifier, the prover computes $y_a$ and the corresponding witness $w$ for proving $y_a = T(a)$, then sends $y_a$ to the verifier.
• This relationship $R = ((ya, a, comT); w)$ is treated as a $NP$ relationship as described above in the ZKP.
• The verifier and the prover then invoke the backend zero-knowledge proofs protocol to verify the relationship $R$ without leaking any information of $T$ except for $y_a$.
• This approach ensures that the privacy of the decision tree is preserved while still allowing for accurate predictions to be made and verified.

Authenticated Decision Tree

The paper introduces the concept of an Authenticated Decision Tree (ADT), which is a decision tree that has been authenticated by a commitment scheme. The ADT is used in the proposed protocols for zero knowledge decision tree predictions and accuracy tests. The ADT is constructed by hashing the root of the decision tree concatenated with a random point, which is used as the commitment.

• A naive approach to committing to a decision tree is to compute the hash of the entire tree, but this would result in high overhead when proving predictions.
• Another approach is to use a Merkle hash tree on all the nodes in the decision tree, but this would still introduce overhead in the zero knowledge proof backend.

Construction of ADT

The paper describes the construction of the ADT, which involves hashing the root of the decision tree concatenated with a random point to produce the commitment. The paper notes that the commitment must be randomized in order to prove the zero knowledge property of the scheme later.

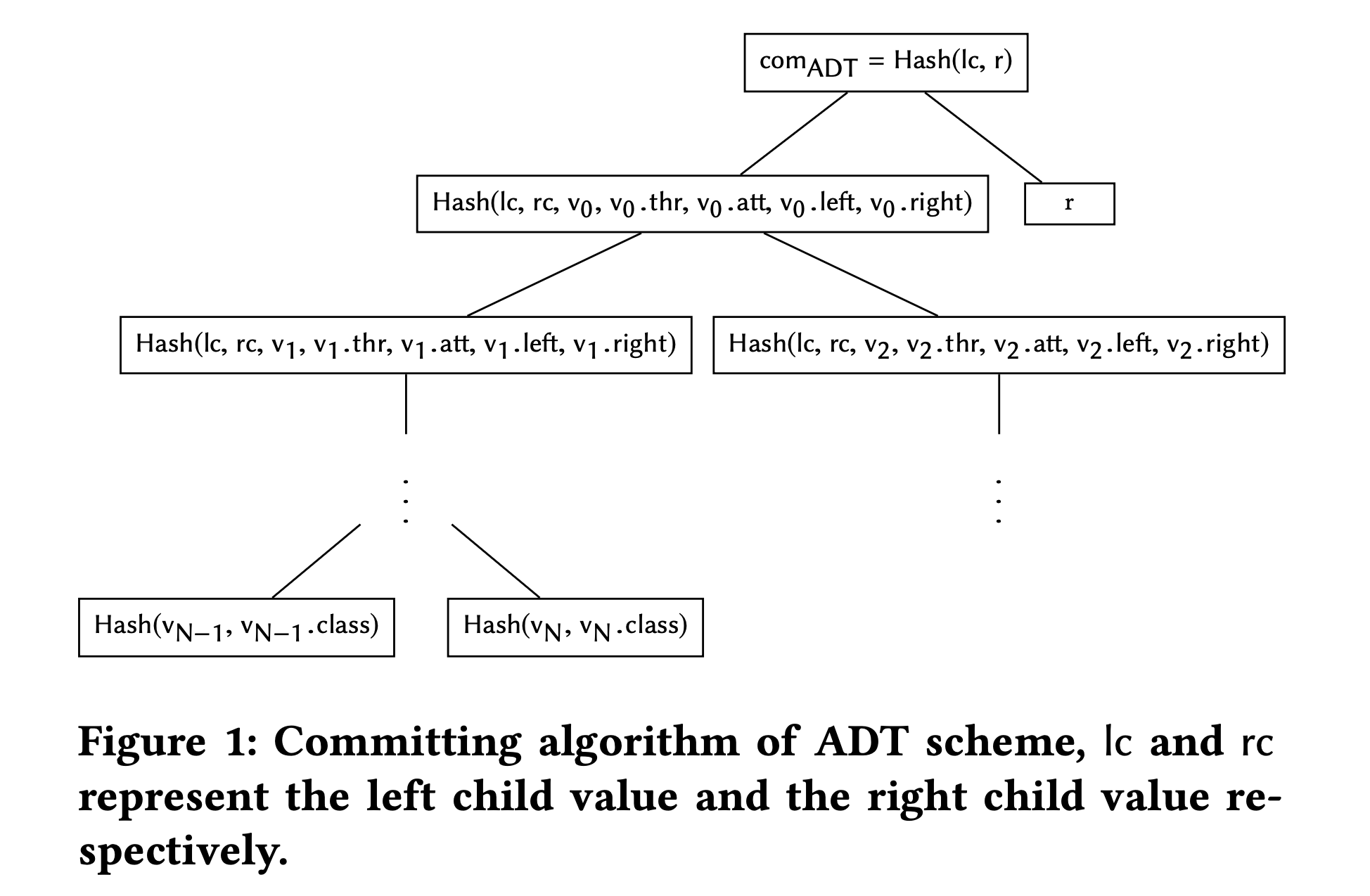
• Each node in ADT contains three pieces of information: the attribute $(v.att)$, the threshold $(v.thr)$, and pointers to the left and right children $(lc, rc)$.
• The construction of ADT is illustrated in the above figure, which shows how the hash of an intermediate node is computed using the hashes of its children and its own attribute and threshold values.
• The inclusion of the attribute and threshold values in the hash computation ensures that the integrity of the decision tree is maintained, and any tampering with the tree structure or values will be detected during verification.
• The verification algorithm for ADT is similar to that of the Merkle hash tree, where the proof includes the prediction path from the root to the leaf node that outputs the prediction result, as well as the hashes of the siblings of the nodes along the prediction path.
• With the proof, the verifier can recompute the root hash and compare it with the commitment to ensure the validity of the prediction.
• The advantage of using ADT over Merkle hash tree is that the verification of ADT only requires $O(h)$ hashes, where $h$ is the height of the decision tree, whereas Merkle hash tree requires $O(h log N)$ hashes, where $N$ is the number of nodes in the tree.
• The construction of zkDT uses ADT to efficiently turn decision tree predictions and accuracy into statements of zero knowledge proofs, which allows the owner of a decision tree model to convince others of its accuracy without revealing any information about the model itself.

With the construction of ADT, we can update our methodology of the algorithms used in the ADT for zero knowledge proofs of decision tree predictions and accuracy.

• In order to prove the zero knowledge property of the scheme, the commitment has to be randomized. This means that a random point $r$ is added to the root of the decision tree and the hash of the root concatenated with r is used as the final commitment. This is shown in the above figure.
• This ADT described in the paper does not have to support dynamic insertions and deletions for the purpose of the application, which simplifies the construction significantly.
• The first algorithm, $pp ← ADT.G(1^λ)$, samples a collision-resistant hash function from the family of hash functions.
• The second algorithm, $comADT ← ADT.Commit(T, pp, r)$, computes hashes from leaf nodes to the root of $T$ with the random point $r$ as shown in the above figure.
• The third algorithm, $πADT ← ADT.P(T, Path, pp)$, given a path in $T$, contains all siblings of the nodes along the path Path and the randomness $r$ in the above figure.
• The fourth algorithm, ${0, 1} ← ADT.V(comADT, Path, πADT, pp)$, given Path and $πADT$, recomputes hashes along Path with $πADT$ as the same progress in the above figure and compares the root hash with $comADT$. It outputs $1$ if they are the same, otherwise, $0$.
• These algorithms are used to efficiently turn decision tree predictions and accuracy into statements of zero knowledge proofs.

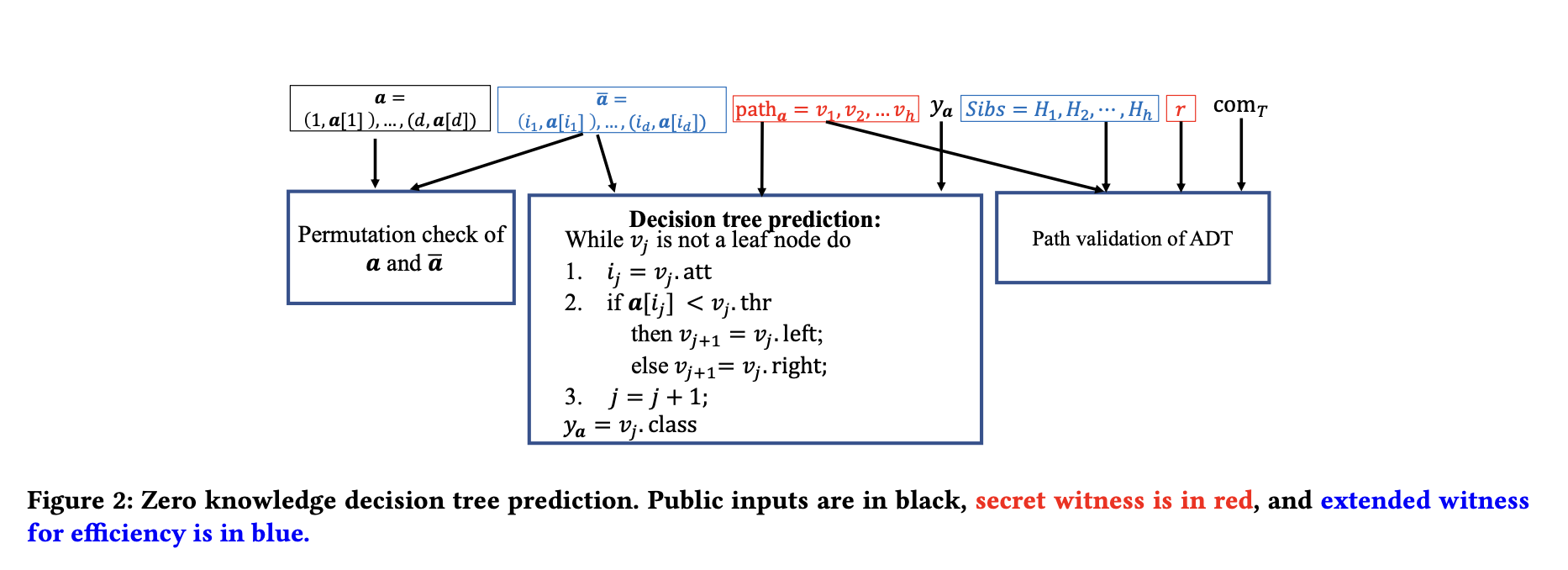
Proving the Validity of the Prediction

The protocol for proving the correctness of the prediction in a decision tree involves using a zero knowledge proof on top of the validation process to keep the prediction path and sibling hashes confidential (zero knowledge). This protocol ensures that the verifier only receives a binary output $(1 or 0)$ indicating whether all the checks are satisfied or not, making it both sound and zero knowledge.

• 

The below steps explain the design of an efficient zero knowledge proof protocol proposed in the paper for validating decision tree predictions.

• The protocol reduces the validity of the prediction using a committed decision tree to an arithmetic circuit.
• The public input of the circuit includes the data sample $a$, the commitment of the decision tree $comT$, and the prediction result $y_a$.
• The secret witness from the prover includes the prediction path $a$ and the randomness $r$ used in the commitment of ADT.
• To improve efficiency, the prover inputs the siblings of nodes on the prediction path and the permutation $\hat{a}$ of the data sample $a$ ordered by $v.att$ of the nodes on the prediction path as part of the witness.
• The purpose of the extended witness is to check the permutation between the data sample and the ordered sample and to validate the prediction path in the committed decision tree.
• The whole circuit consists of three parts: validating the prediction algorithm of the decision tree, checking the permutation between the data sample $a$ and the ordered sample $\hat{a}$, and checking the validity of the prediction path in the committed decision tree.
• The output of the circuit is either $1$ or $0$, denoting whether all the conditions are satisfied or some check fails.

Decision Tree Prediction

The above figure 2 describes the zero knowledge decision tree prediction.

• The validation process is efficiently implemented using an arithmetic circuit with the help of auxiliary input $\hat{a}$.
• The representation of a and $\hat{a}$ is slightly modified to be index-value pairs, where $a = (1, a[1]), . . . , (d, a[d])$ and $a = (i_1, a[i_1]), . . . , (i_d , a[i_d])$.
• The circuit checks for every internal node $v_j$ on the prediction path $(j = 1, . . . , h−1)$ that (1) $v_j.att = i_j$, and (2) if $a[i_j ] < v$j.thr$, $v_j+1 = v_j.left$, otherwise $v_j+1 = v_j.right$.
• The equality tests and comparisons are computed using standard techniques in the literature of circuit-based zero knowledge proof with the help of auxiliary input.
• Finally, the circuit checks if ya = vh .class. The circuit outputs 1 if all the checks pass, and outputs 0 otherwise.
• The total number of gates in this part is O(d + h), which is asymptotically the same as the plain decision tree prediction in Algorithm 1.
• If h < d, which is usually true in practice, the circuit only checks the indices of the first h − 1 pairs in ̄a. The rest of the indices are arbitrary, as long as ̄a is a permutation of a.
• The prover and the verifier can either agree on the length of the prediction path and construct a separate circuit for every data sample, or use the height of the tree as an upper-bound to construct the same circuit for all data samples.
• Both options are supported by the scheme, and the asymptotic complexity is the same. However, the former is more efficient but leaks the length of the prediction paths.

Permuitation Test

Path Validation

Zero Knowledge Decision Tree Prediction Protocol

Zero Knowledge Decision Tree Accuracy

Validating Decision Tree Accuracy

The paper proposes a protocol for validating decision tree accuracy using a zero knowledge proof. The protocol involves the prover generating a proof that the decision tree