- Introduction
- Problem Explanation
- Problem Definition Weighted Set Cover
- Solution Greedy Algorithm
- Implementation in SageMath
- Example Scenario
- Applications in Blockchain Technology and Machine Learning
- Relating to Karp Reduction
- Conclusion
Introduction
Welcome, fellow adventurers, to a captivating journey through the realms of the weighted set cover problem (WSC)! Imagine yourself as a wise ruler of a vast kingdom, yearning to promote tourism and showcase the wonders of your realm. But with a limited budget, how do you ensure that every precious gem in your kingdom receives the attention it deserves? Fear not! The weighted set cover problem comes to your rescue, providing a strategy to maximize coverage while minimizing cost. Let’s embark on this quest together!
Problem Explanation
In this kingdom, attractions are like gleaming gems scattered across the land, and subsets represent different regions or provinces. The goal is to select a set of travel packages (subsets) that cover all the attractions (items) while keeping the total cost (weight) within your budget. Mathematically, we define the weighted set cover problem using set notation and equations. Let $U$ be the set of items, $S$ be the collection of subsets, $w(i)$ be the weight associated with item i, and $B$ be the budget. Our objective is to find a minimum-weight set cover such that the total weight is minimized $(∑w(i)$ for $i$ in $C$) and within the budget $(∑w(i)$ for $i$ in $C ≤ B$).
Now, let’s understand this step by step:
Problem Definition Weighted Set Cover
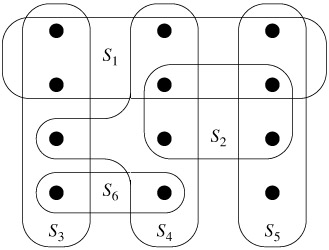
Given:
- A universe $U$ of $n$ items (attractions in our analogy).
- A collection $S$ of m subsets (regions/provinces).
- A weight $w(i)$ associated with each item $i$, indicating its cost.
- A budget $B$.
Find:
- A minimum-weight set cover, which is a collection of subsets that covers all the items in $U$, such that the total weight of the selected subsets is less than or equal to the budget $B$.
Mathematically, we can represent the problem as follows:
Let $U = {1, 2, 3, …, n}$ be the set of items. Let $S = {S₁, S₂, …, Sₘ}$ be the collection of subsets. Let $w(i)$ be the weight associated with item $i$. Let $B$ be the budget.
The objective is to find a set $C$ of subsets such that:
- $C$ covers all items in $U$.
- The total weight of the subsets in $C$ is minimized: $∑w(i)$ for i in $C$ is minimized.
- The total weight of the subsets in $C$ is less than or equal to the budget $B: ∑w(i)$ for $i$ in $C ≤ B$.
To solve this problem, we can use various algorithms, and one popular approach is the greedy algorithm. The idea behind the greedy algorithm is to iteratively select the subset that covers the maximum number of uncovered items while keeping the total weight within the budget. We can repeat this process until all items are covered.
Solution Greedy Algorithm
Imagine you’re accompanied by a knowledgeable tour guide who knows the ins and outs of each region. The guide suggests using the greedy algorithm, a tried-and-true strategy. At each step, the algorithm selects the subset that covers the maximum number of uncovered items, ensuring the greatest coverage for your budget. This iterative process continues until all items are covered. Picture a sequence diagram where the tour guide carefully evaluates subsets and intelligently selects the most promising ones.
Implementation in SageMath
Enter SageMath, your trusty advisor equipped with mathematical prowess! SageMath is a powerful mathematical software that enables us to implement the weighted set cover algorithm with ease. Let’s dive into the code and unravel its secrets.
# Import the required modules
from sage.all import *
def weighted_set_cover(U, S, w, B):
C = [] # Selected subsets
uncovered = set(U) # Initially, all items are uncovered
while uncovered:
best_subset = None
max_covered = 0
for subset in S:
covered = uncovered.intersection(subset)
if len(covered) > max_covered:
best_subset = subset
max_covered = len(covered)
C.append(best_subset)
uncovered -= best_subset
total_weight = sum(w[i] for subset in C for i in subset)
return C, total_weight
In this code snippet, we start by importing the necessary modules from SageMath. The weighted_set_cover function takes four parameters: U (the set of items), S (the collection of subsets), w (the dictionary representing the weights of items), and B (the budget).
Inside the function, we initialize an empty list C to store the selected subsets. We also create a set uncovered containing all the items initially, as none of them are covered.
Next, we enter a loop that continues until all items are covered. Within this loop, we search for the best subset that covers the maximum number of uncovered items. To accomplish this, we iterate through each subset and find the intersection with the uncovered items. If the number of covered items is greater than the previous maximum, we update the best_subset and max_covered variables accordingly.
After selecting the best subset, we add it to our list of selected subsets C and remove the covered items from the uncovered set.
Finally, we calculate the total weight of the selected subsets by summing the weights of the items within each subset in C.
Example Scenario
Let’s consider a whimsical example to bring this problem to life. In your kingdom, you have five enchanting items (1, 2, 3, 4, 5) and four distinct regions or provinces: {1, 2}, {2, 3, 4}, {1, 3, 5}, and {4, 5}. Each item carries a unique weight: item 1 has a weight of 3, item 2 has a weight of 5, item 3 has a weight of 2, item 4 has a weight of 4, and item 5 has a weight of 1. Your budget for promoting these treasures is set at 10.
Let’s invoke our trusty SageMath code to find the optimal solution:
U = {1, 2, 3, 4, 5} # Set of items
S = [{1, 2}, {2, 3, 4}, {1, 3, 5}, {4, 5}] # Collection of subsets
w = {1: 3, 2: 5, 3: 2, 4: 4, 5: 1} # Weight associated with each item
B = 10 # Budget
selected_subsets, total_weight = weighted_set_cover(U, S, w, B)
print("Selected Subsets:")
for subset in selected_subsets:
print(subset)
print("Total Weight:", total_weight)
Executing this code will display the result of our royal decree: the selected subsets and their total weight. The output will provide valuable insights into which regions or provinces you should include in your travel packages to maximize coverage while keeping costs under control.
Applications in Blockchain Technology and Machine Learning
The weighted set cover problem finds its applications in various technological domains, where efficient resource allocation and optimization are crucial. Let’s explore two intriguing examples in the blockchain and machine learning fields.
Blockchain Transaction Fee Optimization
In the realm of blockchain technology, the weighted set cover problem can be employed to optimize transaction fee calculations. In blockchain networks like Bitcoin or Ethereum, users must pay transaction fees to incentivize miners or validators to include their transactions in the next block.
Consider a scenario where a user wants to perform multiple transactions while minimizing the total transaction fee paid. Each transaction corresponds to an item, and the available subsets represent different sets of transactions that can be included in a block. The weights associated with the items can represent the transaction fees.
By solving the weighted set cover problem, blockchain systems can identify the optimal set of transactions to include in a block, maximizing the number of transactions while minimizing the total fee paid by the user.
Machine Learning Feature Selection
Feature selection plays a vital role in machine learning, where the goal is to identify the most relevant features or attributes that contribute to accurate predictions or classifications. The weighted set cover problem can be utilized to solve feature selection challenges efficiently. In Machine Learning, there are different kinds of techniques to identify the best predictors to explain the data.
Imagine a dataset with a large number of features, each representing a potential attribute. By treating the features as items and subsets as different combinations of feature subsets, the weighted set cover problem can help identify the minimal set of features that provide optimal predictive power.
Solving the weighted set cover problem in the context of machine learning allows for efficient feature selection, reducing computational complexity, and improving model performance and interpretability.
These are just two glimpses into the vast applications of the weighted set cover problem in the technological landscape. Whether in blockchain, machine learning, or other domains, this problem provides valuable insights and optimization strategies for resource allocation, decision-making, and problem-solving. As technology advances, the weighted set cover problem continues to contribute to innovative solutions and efficient resource utilization.
Relating to Karp Reduction
The weighted set cover problem has an intriguing connection to Karp reduction, a fundamental concept in computational complexity theory. We can formally express this relationship using mathematical notation.
In computational complexity theory, Karp reduction is denoted by the symbol $\leq_{\text{Karp}}$, indicating that one problem can be reduced to another. In our case, we can demonstrate that the weighted set cover problem is Karp reducible to the Set Cover problem.
Let’s define the two problems mathematically:
- Weighted Set Cover Problem (WSC):
- Given a universe of items $U$, a collection of subsets $S$, weights $w(i)$ for each item $i \in U$, and a budget $B$,
- The objective is to find a minimum-weight set cover $C$ such that $\sum_{i \in C} w(i) \leq B$.
- Set Cover Problem (SC):
- Given a universe of items $U$ and a collection of subsets $S$,
- The objective is to find the smallest collection of subsets $C$ such that $\bigcup_{X \in C} X = U$.
To establish the Karp reduction from the WSC problem to the SC problem, we construct an instance of the SC problem using the same universe $U$ and subsets $S$ as in the WSC problem. Additionally, we assign unit weights to all items in the SC problem.
Formally, we can express the Karp reduction as follows:
$WSC \leq_{\text{Karp}} SC$
This reduction shows that the WSC problem can be transformed into the SC problem, indicating that the WSC problem is at least as hard as the SC problem. Since the SC problem is known to be NP-complete, this implies that the WSC problem is also NP-complete.
Understanding this mathematical relationship between the WSC problem and Karp reduction provides valuable insights into the computational complexity of the problem and establishes connections with other NP-complete problems. It allows us to leverage existing algorithms and problem-solving techniques developed for the SC problem when tackling the WSC problem.
Conclusion
Congratulations! You have successfully embarked on a journey through the fascinating world of the weighted set cover problem. We began our adventure by imagining ourselves as rulers, seeking to promote tourism in our kingdom. We learned about the problem’s formulation using mathematical notation and equations, and we employed the greedy algorithm as our trusted tour guide to select subsets that covered the maximum number of attractions while staying within our budget.
With the help of SageMath, we implemented the weighted set cover algorithm, carefully considering the code’s structure and functionality. We then applied our implementation to an example scenario, where we discovered the optimal subsets and their total weight.
The weighted set cover problem holds great importance in various real-world applications, such as optimization, resource allocation, and data analysis. It provides a valuable framework for decision-making and problem-solving.
As you venture forth, remember to explore further, experiment with different scenarios, and adapt the code to your specific needs. May your kingdom thrive with flourishing tourism and abundant gem-filled travel packages!
Happy covering, noble ruler!
You can find the complete sagemath code at the github repo github.com/thogiti.
Additional References