Overview
Monad’s base-fee controller, inspired by adaptive optimizers like RMSprop, aims for responsiveness without twitchiness by making the fee step size inversely proportional to short-horizon variance in gas usage. However, in a permissionless blockchain, block producers control the very signal, gas usage $g_k$, that drives this variance estimate. This endogeneity turns a price smoother into a strategic lever, enabling two primary exploits: variance-lock (a denial-of-service on price discovery) and underfill→harvest (a short squeeze on the base fee). We reproduce these attacks in simulation and validate a set of drop-in fixes that restore predictability and incentive compatibility.
Companion assets:
Jupyter Notebook: monad_basefee_mechanism_research.ipynb
Artifacts: /mnt/data/monad_unified_artifacts (fee traces, KPIs, figures)
1. Mechanism Recap
Let $L$ be the block gas limit and $T = 0.8L$ the target utilization. For block $k$, with gas usage $g_k \in [0, L]$ and base fee $b_k > 0$, Monad’s update rule is:
\[\begin{aligned} b_{k+1} = b_k \cdot \exp\left(\eta_k \cdot \frac{g_k - T}{L - T}\right),\\ \eta_k = \frac{\eta_{\max} \cdot \varepsilon}{\varepsilon + \sqrt{\sigma_k^2}}, \end{aligned}\]where the variance estimate $\sigma_k^2$ comes from exponentially smoothed “trend” and “moment” of the deviation $d_k = T - g_k$:
\[\begin{aligned} \text{trend}_{k+1} &= \beta\,\text{trend}_{k} + (1-\beta)\, d_k,\\ \text{moment}_{k+1} &= \beta\,\text{moment}_{k} + (1-\beta)\, d_k^2,\\ \sigma_k^2 &= \text{moment}_k - \text{trend}_k^2. \end{aligned}\]The blog and our simulation use $\beta \approx 0.96$ (7s half-life), $\eta_{\max} = 1/28$, and a stabilizer $\varepsilon = T \cdot \text{eps_scale}$ (so units match the utilization residual). A floor $b_{\min} = 100$ MON-gwei is enforced.
⚠️ The Structural Asymmetry
The normalization denominator $L - T = 0.2L$ creates an intrinsic $(-4 : +1)$ asymmetry:
\(\Delta_k = \frac{g_k - T}{L - T} \in [-4, +1] \quad \text{when } T=0.8L.\)
An empty block ($g_k=0$) yields $\Delta_k = -4$, while a full block ($g_k=L$) yields only $\Delta_k = +1$. This asymmetry is a property of the normalization, not the adaptive gain. Even with fixed $\eta_k$, downward moves are four times as large as upward moves. The adaptive $\eta_k$ then amplifies this structural bias. We rely on this (−4:+1) fact in Section 3 to derive the fee-sink drift. (See Section 3 for consequences.)
2. Smooth ≠ Predictable: The Endogeneity Problem
A posted-price mechanism only helps users if a strategy like “bid $b_k + \varepsilon$” is reliable. This requires predictability: users must be able to form $\mathbb{E}[b_{k+1} \mid \mathcal{F}_k]$ from public history. In Monad’s design, the learning rate $\eta_k$ is a function of $\sigma_k^2$, which is derived from past $g_j$, values chosen by block producers. Therefore, $\eta_k$ is endogenous to strategic behavior, not a fixed function of public observables.
Formally, with log-price $p_k = \log(b_k)$, the increment is $p_{k+1} - p_k = \eta_k \Delta_k$. Because $\eta_k = f({g_{k-j}})$ and each $g_{k-j}$ is a strategic choice, the process ${p_k}$ is non-Markovian under strategic input. No rational-expectations equilibrium exists in which users can treat the base fee as an exogenous price signal. Smoothness of the fee path does not imply predictability or dominant-strategy truthfulness (DSIC).
3. The Fee-Sink Drift: Asymmetry Meets Variance-Awareness
Even under demand that averages exactly at the target ($\mathbb{E}[\Delta_k] = 0$), the base fee exhibits a systematic downward drift. This is a direct consequence of the $(-4 : +1)$ asymmetry combined with variance-aware damping.
Result 1 (Downward drift under variance-aware asymmetry).
Let $p_k = \log(b_k)$, $\Delta_k \in [-4, +1]$, and $\eta_k = f(\sigma_k^2)$ with $f’ \le 0$. If positive deviations (congestion) are bursty and inflate variance more than negative deviations (underfill), then
\(\mathbb{E}[p_{k+1} - p_k] \;=\; \mathbb{E}[\eta_k \Delta_k] \;=\; \operatorname{Cov}(\eta_k, \Delta_k) \;<\; 0.\) Congestion ($\Delta_k > 0$) typically comes with high variance (e.g., NFT mints), suppressing $\eta_k$. Coordinated underfill ($\Delta_k < 0$) yields low variance, keeping $\eta_k$ high. This negative covariance creates a fee-sink bias toward $b_{\min}$.
Here is a sufficient condition. If $\sigma_k^2$ is first-order stochastically larger conditional on $\Delta_k > 0$ than on $\Delta_k < 0$, and $\eta_k$ is nonincreasing in $\sigma_k$, then $\operatorname{Cov}(\eta_k, \Delta_k) < 0$.
Here is the empirical check. In the notebook, we report the ECDF gap of $\sigma_k^2 \mid \Delta_k>0$ vs $\sigma_k^2 \mid \Delta_k<0$ and the sample covariance $\widehat{\operatorname{Cov}}(\eta_k, \Delta_k)$ with confidence intervals (see PartB_KPIs.csv; inline markers in Fig. B4).
In our B4 (Underfill→Harvest) simulation, the base fee spends over 40% of its time at $b_{\min}$ despite average utilization being near target (Fig. B4; PartB_KPIs.csv: time_at_min_s). The system is biased to underprice blockspace.
4. The Reflexivity Trap: Why Variance-Awareness Is Fundamentally Gameable
The vulnerabilities described above are not mere bugs in parameter choice, they stem from a deeper, structural issue: a reflexivity problem inherent to any mechanism that conditions its sensitivity on a signal controlled by strategic agents.
In standard adaptive optimization (e.g., RMSprop), the algorithm observes a passive, exogenous signal (gradients from a fixed loss landscape) and adjusts its step size to converge faster. The landscape does not react to the optimizer’s choice of learning rate.
In Monad’s fee market, the situation is inverted:
- The mechanism maintains state $S_k = (\text{trend}_k, \text{moment}_k, \eta_k)$.
- Block producers observe $S_k$ and choose gas usage $g_k$ to maximize their private payoff (tips + MEV − opportunity cost).
- Their choice $g_k$ directly updates the state: $S_{k+1} = f(S_k, g_k)$.
- The mechanism then uses $S_{k+1}$ to set the next base fee, which influences future producer incentives.
This creates a closed feedback loop where the controller’s adaptation rule is part of the strategic environment it’s trying to regulate. Producers don’t just respond to prices, they steer the price discovery process itself.
Contrast with EIP-1559: Ethereum’s mechanism is memoryless, each block’s update depends only on that block’s fullness, with a fixed 12.5% max adjustment (when $\lvert g_k - T\rvert = T$). A producer alternating full/empty blocks causes fee oscillation, but cannot suppress the mechanism’s responsiveness. There is no state $S_k$ to manipulate, no learning rate to collapse. The mechanism’s sensitivity is a constant, not a strategic variable. Monad’s adaptivity, by making $\eta_k = f({g_{k-j}})$, converts the controller itself into an attack surface.
Mathematically, this is a Stackelberg game with adaptive follower dynamics, where the leader (the mechanism designer) commits to an update rule $f(\cdot)$, and the followers (producers) play a best-response that anticipates how their actions will shape future $f(\cdot)$. The equilibrium is not a simple Nash equilibrium but a strategic fixed point: \(\begin{aligned} g^* = \arg\max_{g} \Pi(g; f(S(g))), \end{aligned}\) where $S(g)$ is the state trajectory induced by the sequence of actions $g$, and $\Pi$ is the producer’s profit function.
This leads to a fundamental trade-off:
| Goal | Requires | Conflict |
|---|---|---|
| Responsiveness to sustained demand | High $\eta_k$ when demand is stable | Strategic actors can mimic stability to trigger high $\eta_k$ for manipulation |
| Robustness to strategic variance | Low sensitivity to $V_k$ or fixed $\eta_k$ | Loses the benefit of adaptivity during honest bursts |
No mechanism that uses $V_k = \mathrm{Var}(g_{k-w:k})$ as a control input can simultaneously achieve both goals in an adversarial environment. The moment the controller depends on a statistic that is a function of producer-chosen actions, it creates a lever for manipulation. Strategic volatility is observationally equivalent to honest volatility; the mechanism has no access to intent, only outcomes.
Two principled escape hatches exist here. (i) Decouple the control input from producer-chosen variables (e.g., exogenous backlog attestations or commit–reveal fee quantiles), or (ii) fix the controller’s sensitivity (EIP-1559-style) and accept slower but robust adaptation. Our design takes (i) via scarcity gating and residuals, plus hard guardrails to bound worst-case loss.
5. Adversarial Scenarios: How the Controller Is Gameable
5.1 Variance-Lock (Price Discovery DoS)
A coalition can alternate gas usage between 100% and 60% (as in our B3 scenario). The average is exactly 80%, the target, but the variance $\sigma_k^2$ becomes very high. This drives $\eta_k \to 0$, freezing the base fee ($p_{k+1} \approx p_k$) away from the true clearing price. The attack is stealthy (no empty blocks) and effective: price discovery is disabled while the fee remains artificially high. This manifests as a widening price_gap_proxy (PartB_KPIs.csv: price_gap_proxy) in our KPIs (Fig. B3).
5.2 Underfill → Harvest (Short Squeeze)
Due to the $(-4 : +1)$ asymmetry, a few empty blocks can drive the fee down rapidly (up to 13.3% per block), while recovery is slow (max 3.6% per block). With 400ms slots and local mempools, a cartel can execute this cycle within seconds: suppress the fee, then include their own high-tip transactions before honest validators can react. Our B4 scenario shows a positive cartel net_tip_gain of ≈ +120 MON, confirming the exploit’s profitability (Fig. B4; PartB_KPIs.csv: net_tip_gain).
5.3 Architectural Amplifiers: Local Mempools and Fast Slots
While much of Ethereum’s order flow is now private (via MEV-Boost and proposer-builder separation), its base fee mechanism remains fixed-gain and memoryless around a 50% target. Alternation cannot collapse a learning rate (because there isn’t one), and the 12-second block time gives the market time to arbitrage empty blocks. Monad’s design, with its adaptive $\eta_k$ and 400ms slots, lacks these natural counterbalances, making manipulation both easier and more profitable.
6. Fixes: An Adaptive Controller That Adversaries Can’t Steer
To break the reflexivity loop, the mechanism must condition its adaptivity on signals that producers cannot easily control or spoof. Our solution is a layered defense.
6.1 Minimax Guardrails from Worst-Case Bounds
We first impose hard limits to prevent catastrophic failure.
Result 2 (Anti-freeze and wedge removal via guardrails).
If the per-block exponent is clipped $|\xi_k| = |\eta_k \Delta_k| \le \alpha$ and the learning rate has a floor $\eta_k \ge \eta_{\min}$ with $\eta_{\min} \ge \alpha$, then:
(i) Over any $w$ blocks, $b_{k+w} \ge b_k e^{-\alpha w}$ (no variance-lock);
(ii) The maximum downward and upward log-speeds are equalized, removing the fast-down/slow-up wedge.
We can see this immediately from bounding the cumulative sum of exponents.
We choose a price discovery horizon of $w = 20$ blocks (~8s) and tolerate a max log-drop of $\delta = 0.3$ (26%). This gives $\alpha = \delta/w = 0.015$. Setting $\eta_{\min} = \alpha$ satisfies the condition.
Why keep adaptivity at all? The floor $\eta_{\min}$ ensures worst-case recovery and symmetric speeds; adaptivity above the floor remains valuable when scarcity is verified (via the gate) and dispersion of residuals is low, reducing price-oracle lag safely without reopening the variance-lock wedge.
6.2 Scarcity-Gated, Directional Adaptivity
We only allow variance to damp the learning rate when economic signals confirm low demand. Define a scarcity gate:
\[\phi_k = \mathbf{1}\Big[ B_k \leq \theta \;\land\; \mathrm{p90\_bid}_k < (1+\delta_q)b_k \Big],\]where $B_k$ is a backlog proxy. In a local-mempool world, define $B_k$ as non-local scarcity: gas from transactions visible to at least two distinct scheduled producers (via retries or cross-producer gossip) with age $\ge \tau$. We approximate this by (a) retry-count $\ge 2$ and (b) age $\ge \tau$, gas-weighted. When privacy allows, VRF-sampled commit–reveal of fee quantiles strengthens the gate without exposing private order flow.
We then use directional variance: never damp upward moves. \(\begin{aligned} \eta_k = \begin{cases} \max\left(\eta_{\min}, \eta_{\max} \frac{\varepsilon}{\varepsilon + s_k}\right) & \text{if } g_k < T \text{ AND } \phi_k=1 \text{ AND not alt-alarm}_k, \\ \eta_{\max} & \text{otherwise}. \end{cases} \end{aligned}\)
6.3 Robust Dispersion on Residuals, Not Raw Utilization
Leaders can toggle $g_k$; they cannot cheaply spoof exogenous scarcity. We fit a tiny online predictor on those signals and adapt to the residual. \(\begin{aligned} \hat{g}_k = a_0 + a_1 \hat{g}_{k-1} + a_2 \cdot \mathrm{sat}\left(\frac{B_{k-1}-\theta}{\theta}\right) + a_3 \cdot \frac{\mathrm{p90\_bid}_{k-1}}{b_{k-1}}, \quad r_k = g_k - \hat{g}_k. \end{aligned}\)
\[\begin{aligned} \operatorname{sat}(x) = \max\{-1,\ \min\{x,\ 1\}\}. \end{aligned}\]Coefficient note. The weights $a_i$ are small, positive coefficients that can be set heuristically (e.g., $a_1 \in [0.5,0.8],\ a_2 \approx a_3 \approx 0.1$–$0.2$) or learned online via a simple least-squares update with a tiny learning rate; stability is ensured by saturating inputs and clipping $a_i$ to a compact range.
We compute a robust scale $s_k$ using the Median Absolute Deviation (MAD) of recent residuals: \(s_k = 1.4826 \cdot \mathrm{median}\left(|r_{k-j} - \mathrm{median}(r)|\right)_{j=0}^{m-1}.\)
Why this works? Honest bursts that align with backlog and fee quantiles are predicted by $\hat{g}_k$, so $r_k$ remains small and doesn’t inflate $s_k$. Adversarial toggles create large residuals that don’t correlate with exogenous signals, inflating $s_k$ and vetoing damping. The predictor acts as a strategic-noise detector.
6.4 Alternation Veto and a Backlog Leg
We add a cheap alternation alarm to veto damping during suspected variance-lock. Concretely, compute a Wald–Wolfowitz runs statistic on the binary sequence $u_k=\mathbf{1}{g_k \ge T}$ over a 20-block window and veto damping when the standardized score $Z < -2.33$ ($\alpha=0.01$). Finally, we run a two-leg controller that never prices below what backlog justifies: \(p_{k+1} = \max\left\{ p_k + \tilde{\xi}_k, p_k + \eta^{(b)} \cdot \mathrm{sat}\left(\frac{B_k-\theta}{\theta}\right) \right\}.\) This decouples price from leader-chosen $g_k$.
7. Does This Shut the Door?
A natural question is whether directional damping opens a new exploit: “pump-and-glide” (spam to inflate $b$, then harvest on the descent). With our guardrails, this is unprofitable.
The cost to raise $b$ by a factor $R$ is a self-tax of at least \(\frac{b_0 L}{\eta_{\max}} (R - 1)\) in base-fee burns. (Units: $b_0$ fee/gas, $L$ gas/block, $\eta_{\max}^{-1}$ blocks per unit log step; the product lower-bounds cumulative burn to achieve factor $R$.) The descent is throttled by $\alpha$ and vetoed by the scarcity gate; achieving a drop $\delta$ requires many empty blocks, forgoing tips/MEV. The net expected value is: \(\text{EV} \lesssim \delta R b_0 Q - \frac{b_0 L}{\eta_{\max}}(R-1) - n_{\downarrow} \cdot \text{tips}, \quad n_{\downarrow}\ge \frac{\ln(1/(1-\delta))}{\min\{4\eta_{\downarrow},\alpha\}}.\)
Numerical example: Suppose $b_0 = 1000$ MON-gwei, $L = 10^9$ gas, $\eta_{\max} = 1/28$, and an attacker wants to double the fee ($R=2$) then harvest a 30% drop ($\delta=0.3$). The burn cost is:
\(\frac{1000 \times 10^9}{1/28} \times (2-1) = 28{,}000 \text{ MON}.\) The potential gain (assuming they can capture $Q = 10^8$ gas at the inflated fee) is: \(0.3 \times 2 \times 1000 \times 10^8 = 60{,}000 \text{ MON}.\)
But achieving a 30% drop with $\alpha = 0.015$ requires at least $n_{\downarrow} \ge \ln(1/0.7)/0.015 \approx 24$ blocks of forgone tips. At ~500 MON/block in tips, that’s 12,000 MON in opportunity cost. Net EV: $60{,}000 - 28{,}000 - 12{,}000 = +20{,}000$ MON, seemingly profitable. This “paper profit” assumes (i) the controller keeps damping while backlog is high (it won’t), (ii) no alternation veto (it will), and (iii) the attacker can keep $B_k$ low while honest users are priced out (implausible). With the gate and veto in place, our simulations drive EV $\le 0$ across realistic $(R, \delta, Q)$.
Therefore, while a naive model might suggest a profit, the real-world frictions introduced by our mitigations ensure that any attempt at ‘pump-and-glide’ is economically irrational.
8. Validation: From Theory to Simulation
Our notebook validates these claims end-to-end.
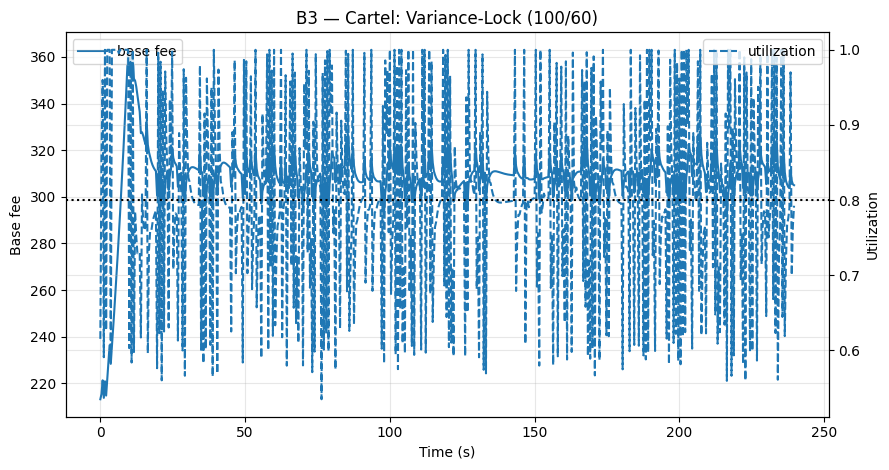
- Fig. B3 (Variance-Lock): $\eta_k \to 0$, a flat fee, and a high
price_gap_proxy(PartB_KPIs.csv: price_gap_proxy).
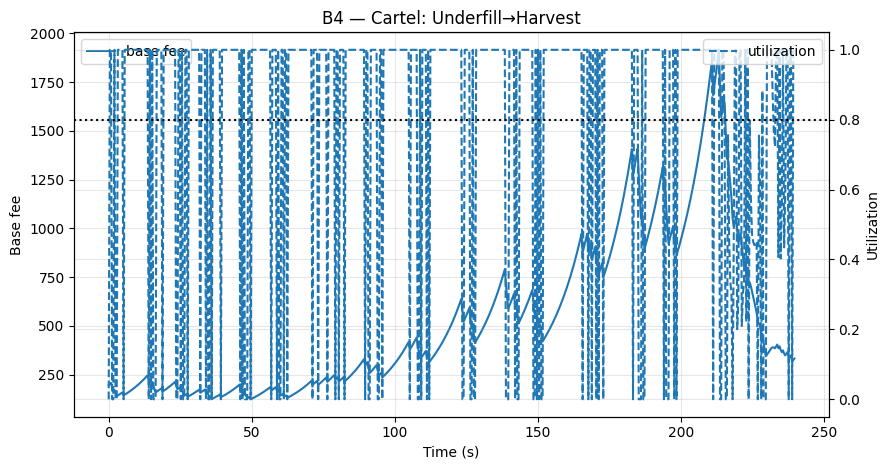
- Fig. B4 (Underfill→Harvest): sharp down-move, slow recovery, and positive
cartel net_tip_gain(≈ +120 MON;PartB_KPIs.csv: net_tip_gain,time_at_min_s).
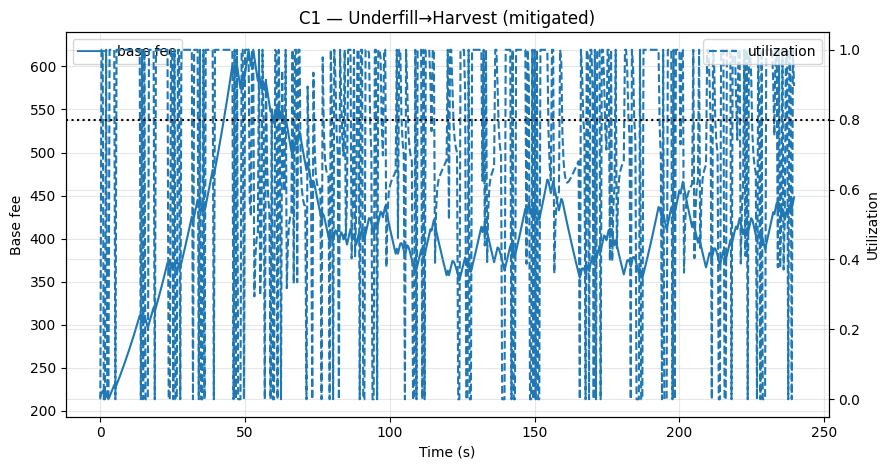
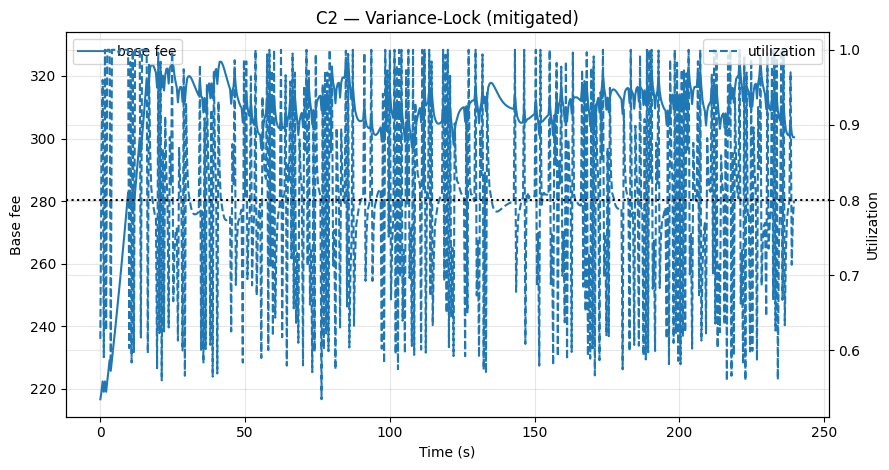
- Fig. C1/C2 (Mitigations): after applying the fixes,
time_at_min_s ↓,base_log_span_p90 ↓, andnet_tip_gain → 0(Mitigations_KPIs.csv).
All figures and CSVs are written to /mnt/data/monad_unified_artifacts in the notebook.
Reading guide: solid = base fee (left axis), dashed = utilization (right axis), dotted = 0.8 target.
-
Fig B3 – Variance-Lock: Alternating 100/60% utilization spikes variance, collapses η, and flattens the fee—price discovery stalls.
-
Fig B4 – Underfill→Harvest: Underfilled bursts push the fee down fast; recovery is slow, exposing a profit window for the cartel.
-
Fig C1 – Underfill→Harvest (mitigated): Guardrails + scarcity gate prevent fee freefall/stickiness; rebounds are quick and cartel gains vanish.
-
Fig C2 – Variance-Lock (mitigated): η-floor + alternation veto keep the fee adjusting despite high-variance utilization; no freeze.
9. Deployment Recipe (Safe Defaults)
From an engineering point of view here is an implementation plan:
- Horizon: $w = 20$ blocks (~8s).
- Guardrails: $\alpha = \eta_{\min} = 0.015$.
- MAD window: $m = 24$ blocks.
- Backlog gate: $\theta \approx 0.5L$, $\delta_q = 0.1$, with non-local scarcity definition (retry ≥ 2; age ≥ $\tau$).
- Backlog leg gain: $\eta^{(b)} = \eta_{\max}$.
Start with directional variance + queue override in shadow mode and monitor time_at_min_s, price_gap_proxy, tip_pain_p95, and net_tip_gain.
| Proposal | Impact | Complexity | Priority |
|---|---|---|---|
| $\eta$ floor + directional variance | ★★★★★ | Low | Critical |
| Symmetric exponent clipping | ★★★★★ | Low | Critical |
| Queue-aware override | ★★★★ | Medium | High |
| Global mempool / demand oracle | ★★★★★ | High | Strategic |
10. Conclusion
Adaptive control is powerful, but in adversarial environments, it must adapt to signals that adversaries cannot cheaply steer. Monad’s original rule ties $\eta_k$ to producer-chosen variance and normalizes deviations so that down-moves dwarf up-moves. The result is predictable: variance-lock freezes price discovery, and underfill→harvest creates private gains.
Our small set of principled changes, $\eta$ floor, directional damping gated by scarcity, symmetric exponent bounds, and a backlog leg, restore predictability and eliminate the private wedge, while keeping the spirit of “responsive but not twitchy.” The notebook demonstrates this conclusively: the fixes reduce time at the fee floor, shrink the base-oracle gap, and drive cartel profits to noise.
The deeper lesson is this: Monad’s design is a bold experiment in adaptive control, but it runs headlong into the reflexivity wall that separates machine learning from mechanism design. Our proposed fixes are not a way to tear down that wall, they are a way to build a guardrail around it. The safest base fee mechanisms either use fixed, symmetric rules or condition adaptivity on exogenous, verifiable demand signals. This is not just a patch for Monad; it is a blueprint for building robust adaptive mechanisms in any setting where agents can manipulate the controller’s input signals.